
서론
지난 포스팅에서는 다이나믹 프로그래밍을 이용한 문제풀이를 했다. 이번에도 dp를 이용한 문제를 풀 것이다. 원래 그리디를 이용해서 풀어야 되는데, 아무리 생각해도 그리디는 방법이 떠오르지 않는다. 하루를 이걸로 보낸 거 같다. 물론 책상에서 이거만 처다본건 아니지만 말이다. 이번 포스팅에서는 dp를 이용해 평범한 배낭(안 평범 하잖슴~) 문제를 파이썬을 이용해 풀어보도록 하겠다. BOJ 12865 문제는 여기로 가면 된다.
BOJ12865 풀이 과정
일단 문제 이해는 쉽다. 각 물품마다 가치와 무게가 있는데 k무게 안에서 가치가 가장 큰 물품들의 가치 총합을 알아내는 것이다. 주의해야 할 것은 우리가 가치가 큰 순서대로 넣는다거나, 혹은 무게가 작은 순서대로 정렬을 하는 것은 쓸모가 업다는 것이다. 문제에서 그 반례가 바로 나온다. 아무튼 이걸 해결하는 과정은 다음과 같다.
- 담아야 되는 물건이 k 무게보다 무거우면 담을 수 없는 상태이므로 dp에는 업데이트 하지 않은 값을 넣어준다.
- 1.이 아닌경우(=넣을 수 있는 경우)는 담아야 되는 물건을 담았을 때와, 아닐 때를 비교를 한 뒤 더 가치가 큰 값을 채택해서 최대 가치를 담는다.
- 마지막에 있는 값을 출력한다.
BOJ12865 코드
n, k = map(int, input().split())
arr = [(0,0)]
for i in range(n):
weight, value = map(int, input().split())
arr.append((weight, value))
dp = [[0]*(k+1) for _ in range(n+1)]
for i in range(1, n+1):
weight, value = arr[i]
for j in range(1, k+1):
if j < weight:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight] + value)
print(dp[n][k])
이번 문제는 단순히 코드만 보면 이해가 가지 않아서 추가 설명을 하겠다. 우선, dp = [[0]*(k+1) for _ in range(n+1)]이 윗부분은 n, k받은 후, 각 인풋을 arr에 넣는 과정과, dp를 k, n길이 만큼 만든 상황이다. 엄밀히 말하면 n+1행 k+1열인데 0행과 0열은 쓰지 않으므로. 사실상 n행 k열이라 하겠다. 이 때 잊지 말아야 될 것은 n은 받는 아이템의 개수이고 k는 최대 무게라는 것이다. 이렇게 만든 이유는 위에 풀이 과정 2번에서 담아야 되는 물건을 담았을 때와 아닐 때의 가치를 비교를 한다고 했기 때문이다. 가치를 비교하려면 d[?][?]의 값이 가치여야 되는건 당연하다. 그렇기에 dp[x][y] 값은 현재의 가치의 합가 되어야 되고, x든 y든 둘중 하나는 현재의 무게, 다른 하나는 무게의 합을 넣어야 되기 때문이다.
BOJ12865 코드 풀이 이어서 1
이제 아래 코드에 대해서 말을 해보자. weight, value는 각각 현재 arr에서 빼낸 무게와 가치이다. 이걸 1부터 k+1까지 넣어가며 1.과 같이 내가 받은 무게(=weight) 가 k보다 크다면 안 넣는 걸로 하고 그때 가치 최대 값은 이전 가치의 최대 값으로 만든다. dp[n][k] = dp[n-1][k] (= n-1번째 아이템을 넣은거라고 n번째 물품을 넣은거랑 선언함으로써 안 넣으셈 되는 거). 만약 넣을 수 있는 상황이면 (=else:), 현재 아이템을 안 넣었을때와(=dp[n-1][k]) {k에서 내가 넣으려는 무게(=weight)가 빠졌을 때 value + 현재 가치를 넣었을 때의 합} 비교해서 더 큰 수에 현재의 value를 넣는다.) - 빨간색 볼드친 것끼리 비교하면 된다는 말이다. 가독성이 떨어져보여서 빨간색으로 표기했다. dp[n-1][k] 까지는 무리없이 이해가 가는데 현재 무게인 weight을 빼는건 이해가 안 갈 수 있다. 그래서 그림으로 정리를 해 보았다.
BOJ12865 코드 풀이 이어서 2

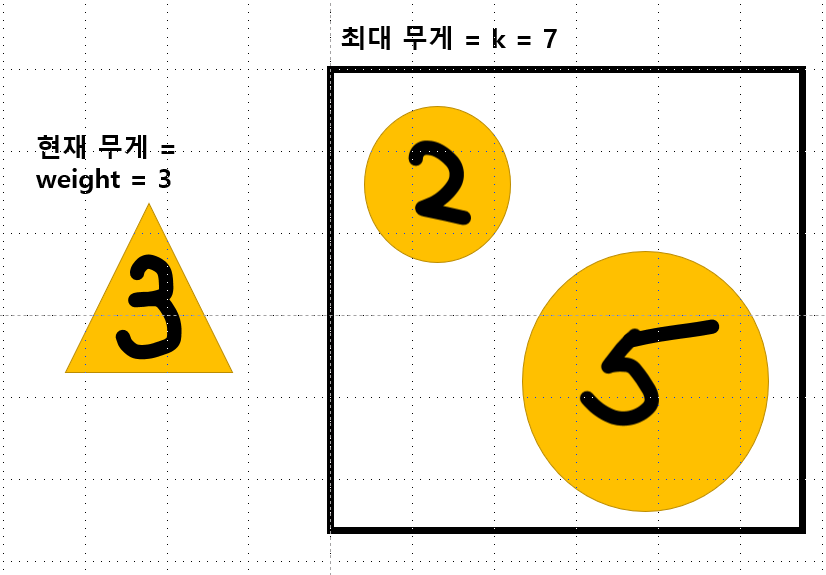
얘는 지금 3을 못집어 넣는 건데, 왼쪽 경우에는 max(d[n-1][7], d[n-1][4])를 하게 된다. d[n-1][4]는 무게가 4라서 0일 것임. 그리고 오른쪽의 경우는 5가 나중에 들어온 케이스다. max(d[n-1][7]과 d[n-1][4])를 하게 된다. 무게가 4면 2가 들어온 상태이므로 무게2의 가치+현재의 가치와 5대신 3을 넣었을때를 비교하는 것이다. 그걸 그림으로 표현하면 다음처럼 된다.


그렇다. 넣는 순서에 따라서 뺄수있는 놈과 비교하는 놈이 달라진다. 항상 최대 값을 뱉어내는 구조상 결과적으로 d[n][k]에 도달했을때는 결과가 같다고 할 수 있다. 이걸 표로 정리를 해보자. 이건 원본 문제 인풋으로 하겠다. 첫번째 경우는 인풋이 [6,13], [4,8],[3,6],[5,12]고 두번째 경우는 [6,13],[3,6],[4,8],[5,12]로 각각 n= 4, k=7로 할 것이다. 해당 dp를 도표로 그려보면
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 6, 13 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 13 |
| 4, 8 | 0 | 0 | 0 | 0 | 8 | 8 | max(8,13) | max(14,13) |
| 3, 6 | 0 | 0 | 0 | 6 | max(6,8) | max(6,8) | max(0,13) | max(8,14) |
| 5, 12 | 0 | 0 | 0 | max(0,6) | max(0,6) | max(12,8) | max(12,13) | max(12,14) |
두번째 상황은 아래 표와 같다. 이전 행의 max값이라고 하면 더 이해하기 쉬울 것 같아서 아래는 max(weight,0)이라고 표현했다. 이걸 작성하다도면 위 행의 max값과 비교하지만 사실 이전 모든 행의 max값과 비교한다는 사실을 알 수 있다. 여전히 이해가 가지 않는다면 그냥 한번 작성해보길 바란다. 위 코드에서는 i, j인데 이게 그때 허용한 k(최대무게)와 그때 넣은 아이템(n)을 의미해서 위에 설명엔 n, k라고 적었으니 참고 요망. 이상으로 백준 12865 풀이를 마치겠다.
'IT, Digital' 카테고리의 다른 글
| [백준] BOJ 1012, 유기농 배추 파이썬 Python (0) | 2025.02.12 |
|---|---|
| [백준] BOJ 11399, ATM Python (0) | 2025.02.09 |
| [백준] BOJ1463, 1로 만들기 (0) | 2025.02.05 |
| [백준] BOJ2566, 최댓값 (0) | 2025.01.14 |
| [백준] BOJ1316, 그룹 단어 체커 (0) | 2025.01.13 |